Using information and data from Monte-Carlo simulations allowed me to make better decisions than just following my gut feeling.
In our evolutionary history, survival often depended on rapidly processing vast amounts of information to navigate the dangers of the world around us. We evolved cognitive shortcuts and assumptions to swiftly assess threats, allowing us to evade predators and remain on step ahead of rival tribes. These mechanisms persist today, and we get a strong gut feeling about things that may not always be useful in the modern world. I fell victim of this gut feeling when first considering this blog but in the modern world we have access to an array of statistical tools and information that our ancestors didn’t, and we can use these to better inform our decision making.
When originally composing this blog about counting cards in the game Play Your Cards Right, I thought it would be a romanticised blog about the underdog combining the art of card counting with their statistical knowledge to help in beating the casinos of Las Vegas. Surely with more information and a bit of knowledge of probability you could start to stack the odds in your favour?
Play Your Cards Right
At the recent PSI conference, Exploristics set up a game “Play Your Cards Right.” In this game, contestants are presented with a sequence of cards, and they must predict whether the next card will be higher or lower in value than the preceding one. A simple game but with many fascinating statistical insights when you delve beneath the surface!
Monte-Carlo simulations are an ideal technique to quantify the impact a player could gain from using a card counting strategy. This approach considers all possible combinations of card distributions, player decisions, and chance events, thereby offering a comprehensive assessment effectiveness of the strategy. At Exploristics we also use Monte-Carlo simulations in KerusCloud to inform complex clinical trial designs to maximise the probability of success through evaluating a vast array of study designs options, risk factors and “what-if” scenarios.
Simulations can lead to surprising insights
When I simulated the game, I found “Counting Cards” strategy was only marginally better than an “educated guess” strategy (using only information from the previous drawn card). So shocked at this outcome, I started to debug my code looking for where I’d made an error. After convinced myself there were no errors in my code, I began to think about my gut feeling and it started to dawn on me this outcome made perfect sense. I’ve advocated data-driven decision making in the past and I was falling foul of not following my own advice!
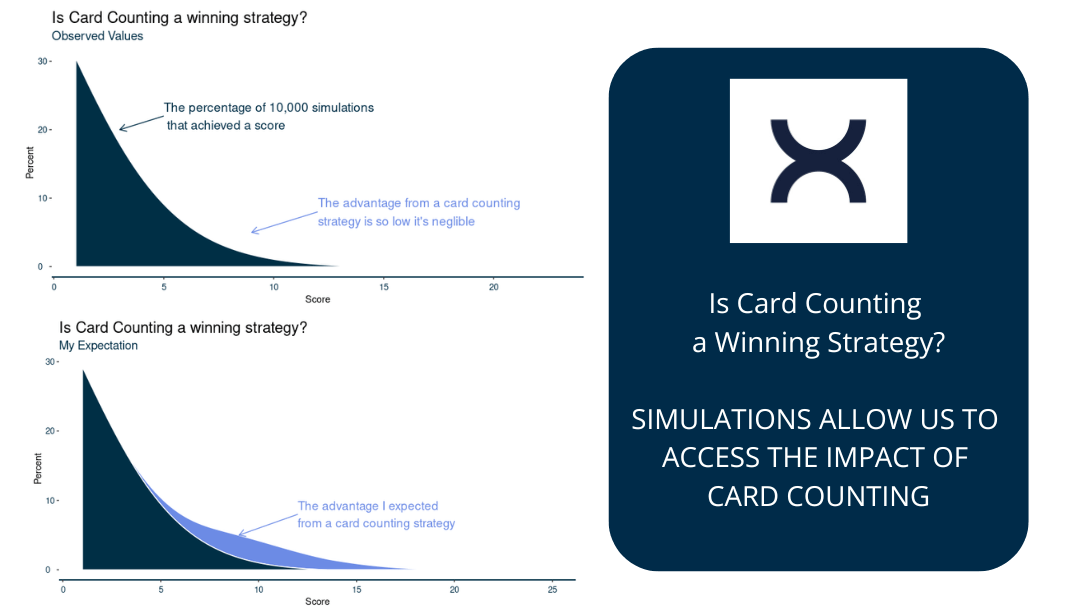
So why was this the case? In my mind’s eye I had a scenario where I had turned over a 7 following a series of high cards – let’s say 9 cards higher than a 7 for the purposes of this analogy. If I wasn’t counting cards and only had knowledge of my previous card, I’d be inclined to guess higher as I know in a full deck there are 28 out of the 51 cards which are higher. But with a card counting strategy I know there’s 42 cards remaining of which 20 (48 %) are lower, 3 are the same (7 %) and 19 are higher (45 %).

So far this is fitting in with my gut feeling, but why weren’t my simulations playing out that way? If you randomly shuffle a deck of cards the odds of getting a specific scenario are 1 in 1068 or if you randomly selected an atom from all the know planets, galaxies and solar systems you were given the one at the end of your finger. Although individual card sequences are just as likely as each other and each sequence also highly unlikely, it needs to be considered in the context of card combinations. If we were to draw 5 high cards higher than a 7 in a row, there’s now relatively more cards lower than a 7 in the deck. So our 6th ,7th, 8th and 9th cards have increasingly greater odds of being a card lower than a 7.
| Next Card in Sequence | ||||
| Outcome | 6th | 7th | 8th | 9th |
| Higher | 22 (49%) | 21 (48%) | 20 (47%) | 19 (45%) |
| Same | 3 (7%) | 3 (7%) | 3 (7%) | 3 (6%) |
| Lower | 20 (44%) | 20 (45%) | 20 (47%) | 20 (48%) |
Table 1: The number of cards that are higher, lower or identical in the deck to the hard card in the number in the drawn sequence
Data-driven decision-making
The most likely event is that we get a mix of high and low cards and card counting strategy and the naive probabilistic strategy result in the same prediction.
“The marginal gains achieved through counting cards are outweighed by the inherent randomness of the game”
The marginal gains achieved through counting cards are outweighed by the inherent randomness of the game. This results in minimal practical impact of our strategy whereby we’d need to play thousands of games to see the benefit.
Whilst card counting does provide a marginal gain in the probability of success, we need to consider the cost-benefit of such an approach. The incremental gain in remembering each additional card is overshadowed by the probability of making a wrong prediction. This could be the difference between success and failure in a rare number of situations but by gathering the data and running simulations we can make better decisions compared to relying on our gut feeling and intuition.
Working in clinical trials, we’re increasingly surrounded by larger datasets and with decreasing profit margins, whereby making optimal decisions is more important than ever. Monte-Carlo simulations provide a decision support tool to turn these data into insight, allowing you to leverage the power of your data resources, increase the probability of success of your trials and gain a cutting edge in a competitive market.
Find out how Exploristics use Monte-Carlo simulations in KerusCloud to aid in study design in clinical trials.




